Video: Si e dini se kur duhet të përdorni produktin ose rregullin e koeficientit?
2024 Autor: Miles Stephen | [email protected]. E modifikuara e fundit: 2023-12-15 23:40
Ndarja e funksioneve.
Pra, sa herë që shihni shumëzimin e dy funksioneve, Rregulli i përdorimit të produktit dhe në rast të ndarjes përdorni rregullin e herësit . Nëse funksioni ka edhe shumëzim edhe pjesëtim, vetëm përdorni të dyja rregullat në përputhje me rrethanat. Nëse shihni një ekuacion të përgjithshëm është diçka si,, ku është një funksion për sa i përket vetëm.
Në mënyrë të ngjashme, dikush mund të pyesë, si e dini se kur duhet të përdorni rregullin e produktit?
Të rregulli i produktit është nëse dy "pjesët" e funksionit janë duke u shumëzuar së bashku, dhe zinxhiri rregull është nëse janë duke u kompozuar. Për shembull, për të gjetur derivatin e f(x) = x² sin(x), ju përdorni rregullin e produktit , dhe për të gjetur derivatin e g(x) = sin(x²) ju përdorni zinxhirin rregull . E shihni ndryshimin?
Në mënyrë të ngjashme, si e dalloni rregullin e produktit? Të rregulli i produktit përdoret kur duke diferencuar dy funksione që shumëzohen së bashku. Në disa raste do të jetë e mundur thjesht t'i shumëzoni ato. Shembull: diferenconi y = x2(x2 + 2x − 3).
Njerëzit pyesin gjithashtu, cili është ndryshimi midis rregullit të produktit dhe rregullit të koeficientit?
Të Rregulli i produktit thotë se derivati i a produkt i dy funksioneve është funksioni i parë shumëfishi i derivatit të funksionit të dytë plus funksioni i dytë shumë i derivatit të funksionit të parë. Të Rregulli i produktit duhet të përdoret kur derivati i herësi duhet marrë nga dy funksione.
Cila është formula për rregullin e produktit?
Të rregulli i produktit Eshte nje formulë përdoret për të gjetur derivatet e produkteve të dy ose më shumë funksioneve. (uv)'=u'v+uv'. Δ(uv)=u(x+Δx)v(x+Δx)−u(x)v(x). ku Δu dhe Δv janë përkatësisht rritjet e funksioneve u dhe v.
Recommended:
Si e përdorni rregullin e produktit dhe koeficientit?
Rregulli i produktit thotë se derivati i një produkti të dy funksioneve është funksioni i parë shumëfishi i derivatit të funksionit të dytë plus funksioni i dytë shumë i derivatit të funksionit të parë. Rregulli i produktit duhet të përdoret kur duhet të merret derivati i herësit të dy funksioneve
Si e përdorni rregullin e dorës së djathtë për produktin kryq?
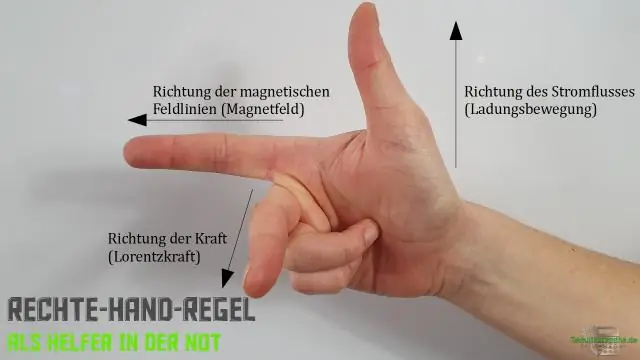
Rregulli i dorës së djathtë thotë se orientimi i prodhimit kryq të vektorëve përcaktohet duke vendosur dhe nga bishti në bisht, duke e rrafshuar dorën e djathtë, duke e shtrirë atë në drejtim të dhe më pas duke rrotulluar gishtat në drejtimin që bën këndi. Gishti i madh tregon më pas në drejtim të
Si e konvertoni rregullin e koeficientit në rregullin e produktit?
Rregulli koeficient mund të shihet si një aplikim i rregullave të produktit dhe zinxhirit. Nëse Q(x) = f(x)/g(x), atëherë Q(x) = f(x) * 1/(g(x)). Ju mund të përdorni rregullin e produktit për të diferencuar Q(x) dhe 1/(g(x)) mund të diferencohet duke përdorur rregullin e zinxhirit me u = g(x) dhe 1/(g(x)) = 1/u
A mund të përdorni rregullin e produktit në vend të rregullit të koeficientit?
Ka dy arsye pse rregulli i herësit mund të jetë superior ndaj rregullit të fuqisë plus produktit në diferencimin e një koeficienti: Ruan emëruesit e përbashkët kur thjeshton rezultatin. Nëse përdorni rregullin e fuqisë plus rregullin e produktit, shpesh duhet të gjeni një emërues të përbashkët për të thjeshtuar rezultatin
Kur duhet të përdorni korrelacionin dhe kur duhet të përdorni regresionin e thjeshtë linear?
Regresioni përdoret kryesisht për të ndërtuar modele/ekuacione për të parashikuar një përgjigje kyçe, Y, nga një grup variablash parashikues (X). Korrelacioni përdoret kryesisht për të përmbledhur shpejt dhe në mënyrë koncize drejtimin dhe forcën e marrëdhënieve midis një grupi prej 2 ose më shumë ndryshoresh numerike