Përmbajtje:
Video: Cili është funksioni i anasjelltë në llogaritje?
2024 Autor: Miles Stephen | [email protected]. E modifikuara e fundit: 2023-12-15 23:40
Në matematikë, një funksioni i anasjelltë (ose anti- funksionin ) Eshte nje funksionin që “përmbys” një tjetër funksionin : nëse funksionin F aplikuar në një hyrje x jep një rezultat të y, pastaj duke aplikuar atë funksioni i anasjelltë g në y jep rezultatin x, dhe anasjelltas, d.m.th., f(x) = y nëse dhe vetëm nëse g(y) = x.
Si rrjedhim, si e gjeni inversin e një funksioni në llogaritje?
Gjetja e anasjellësit të një funksioni
- Së pari, zëvendësoni f(x) me y.
- Zëvendësoni çdo x me një y dhe zëvendësoni çdo y me një x.
- Zgjidheni ekuacionin nga hapi 2 për y.
- Zëvendëso y me f−1(x) f − 1 (x).
- Verifikoni punën tuaj duke kontrolluar që (f∘f−1)(x)=x (f ∘ f − 1) (x) = x dhe (f−1∘f)(x)=x (f − 1 ∘ f) (x) = x janë të dyja të vërteta.
cili është shembulli i funksionit të anasjelltë? Funksionet e anasjellta , në kuptimin më të përgjithshëm, janë funksione që “përmbysin” njëra-tjetrën. Për shembull , nëse f merr a në b, atëherë the anasjelltas , f − 1 f^{-1} f−1f, mbishkrimi i fillimit, minus, 1, mbishkrimi fundor, duhet të marrë b në a.
Këtu, si i dalloni funksionet e anasjellta?
Derivatet e funksioneve trigonometrike të anasjellta
- Përdorni teoremën e funksionit të anasjelltë për të gjetur derivatin e g(x)=sin−1x.
- Meqenëse për x në intervalin [−π2, π2], f(x)=sinx është inversi i g(x)=sin−1x, filloni duke gjetur f′(x).
- f′(x)=cosx.
- f′(g(x))=cos(sin−1x)=√1−x2.
- g′(x)=ddx(sin−1x)=1f′(g(x))=1√1−x2.
Çfarë është një funksion i anasjelltë i vetvetes?
A funksioni i vetë inversit Eshte nje funksionin f, e tillë që y=f(x), me vetinë speciale që ff(x)=x, ose shkruhet në një mënyrë tjetër, f(x)=f−1(x)
Recommended:
Cili është funksioni i vazhdueshëm në llogaritje?
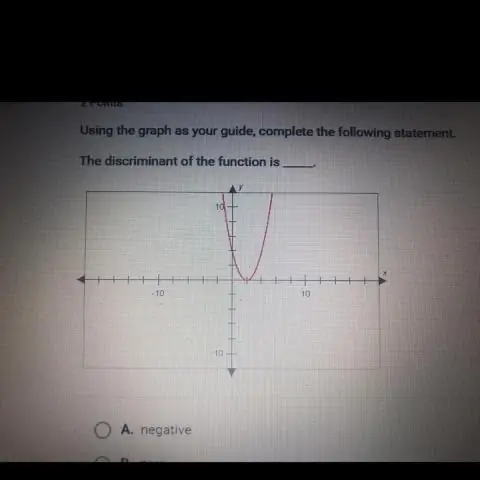
Nëse një funksion është i vazhdueshëm në çdo vlerë në një interval, atëherë themi se funksioni është i vazhdueshëm në atë interval. Dhe nëse një funksion është i vazhdueshëm në çdo interval, atëherë ne thjesht e quajmë atë një funksion të vazhdueshëm. Llogaritja në thelb ka të bëjë me funksionet që janë të vazhdueshme në çdo vlerë në domenet e tyre
Cili është veprimi i anasjelltë i katrorit të një numri?
Veprimi i anasjelltë i kuadrimit të një numri është gjetja e rrënjës katrore të një numri. Rrënja katrore anulon katrorin. Për shembull, 3² = 9. Për të anuluar katrorin, duhet të marrim rrënjën katrore
Për çfarë përdoret ligji katror i anasjelltë?
Në fotografinë dhe ndriçimin e skenës, ligji i kundërt i katrorit përdoret për të përcaktuar 'rënien' ose ndryshimin në ndriçimin e një subjekti ndërsa lëviz më afër ose më larg burimit të dritës
Çfarë është D në llogaritje?
Vetë d thjesht qëndron për të treguar se cila është ndryshorja e pavarur e derivatit (x) dhe cili është funksioni për të cilin merret derivati (y)
Çfarë është një funksion i përbërë në llogaritje?
Kombinimi i dy (ose më shumë) funksioneve si ky quhet kompozim i funksioneve dhe funksioni që rezulton quhet funksion i përbërë. Rregulli i funksionit të përbërë na tregon një mënyrë më të shpejtë. Rregulli 7 (Rregulli i funksionit të përbërë (i njohur gjithashtu si rregulli i zinxhirit)) Nëse f(x) = h(g(x)) atëherë f (x) = h (g(x)) × g (x)